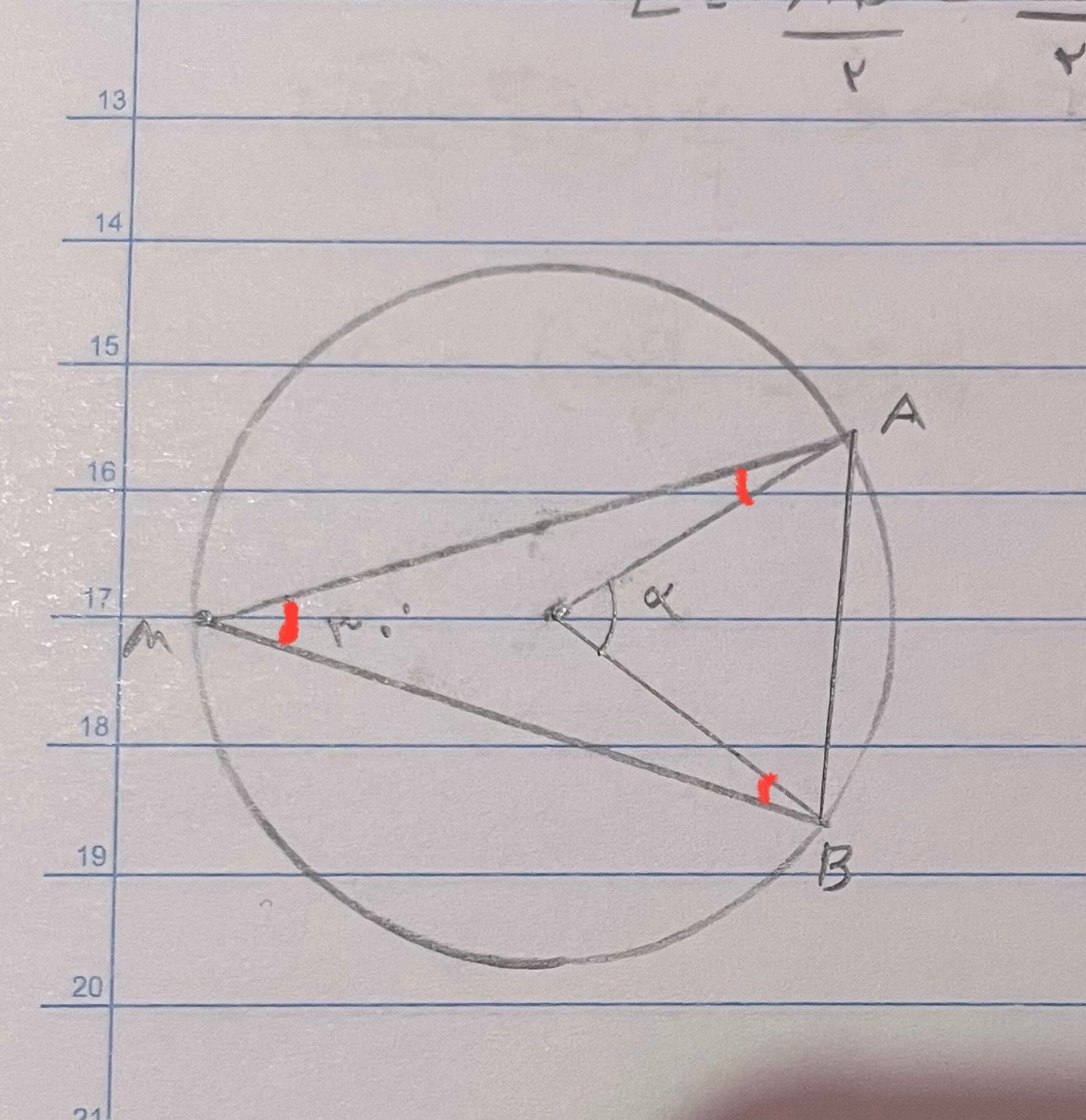
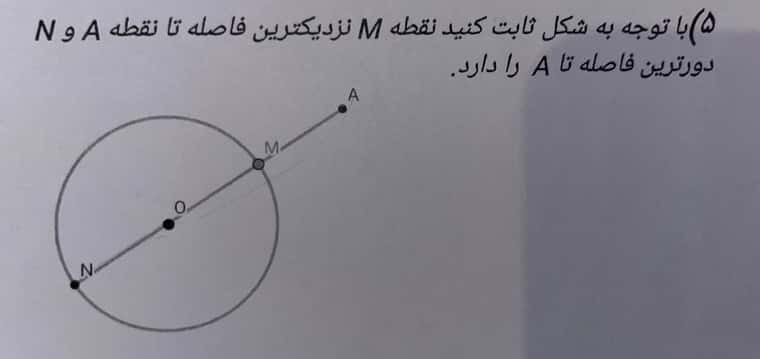
دور ترین و نزدیک ترین فاصله نقطه از دایره
-
سلام، این روش ها برای اثبات به ذهنم اومد:
برای اثبات اینکه نقطه M نزدیک ترین فاصله هست به شکل زیر عمل میکنیم:
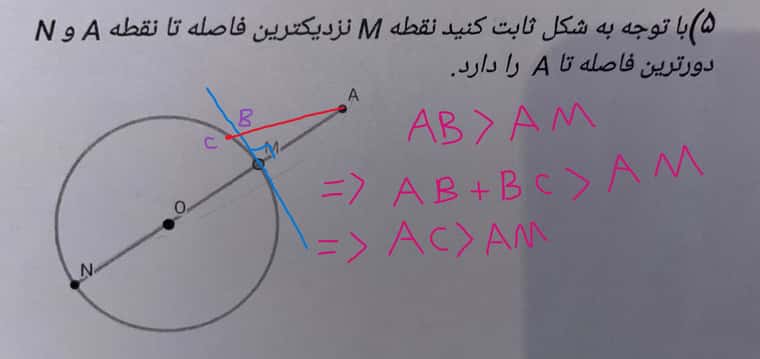
خط مماس بر دایره که از نقطه M میگذره رو رسم میکنیم، میدونیم این خط بر AN عموده، حالا اینجا میایم ادعا میکنیم که این نقطه نزدیک ترین نقطه هست، برای اثبات این موضوع میایم نقطه C رو که یه نقطه دلخواه یه جای دیگه دایره هست فرض میکنیم، میگیم چون AB وتره مطابق شکل، پس از AM بزرگتره، پس AB + یه چیز دیگه که اینجا CB هست هم از AM بزرگتره، پس AC از AM بزرگتره، در نتیجه AM کوچیترین فاصله هست.
.
.
برای اثبات دورترین بودن N هم میشه از راه حل زیر رفت:
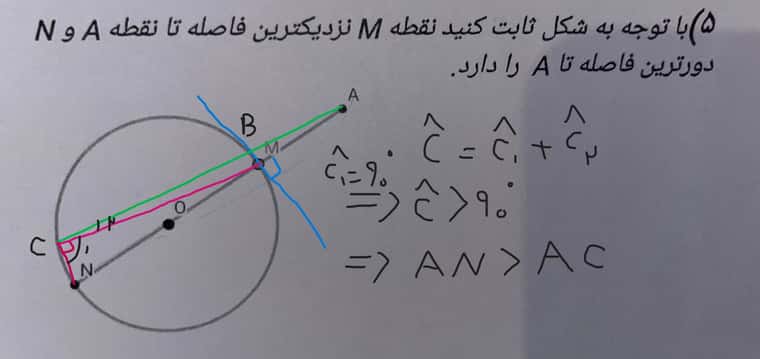
فکر کنم همه چی مشخصه، ولی خب، مطابق شکل خطی رو به دایره که از نقطه M میگذره مماس میکنیم، C یه نقطه فرضی دیگه هست روی دایره، C رو به M وصل میکنیم تا مثلث CNM ساخته بشه، با زاویره C1، خب اینجا C1، نود درجه هست، چون زاویه محاطی هست و کمان رو به روش 180 درجست... C اینجا تشکیل شده از C1 که نود درجه هست و یه زاویه دیگه به اسم C2، پس در نتیجه زاویه C بزرگتر از 90 هست پس درنتیجه بزرگترین زاویه مثلث ACN هست، طبق قضیه ضلع و زاویه برتر، AN بزرگتر از AC هست، پس N دورترین نقطه از A روی دایره هست.
.
.
هرچند روش دومی هم به ذهنم رسید برای اثبات دومی، میشه از روابط طولی استفاده کرد:
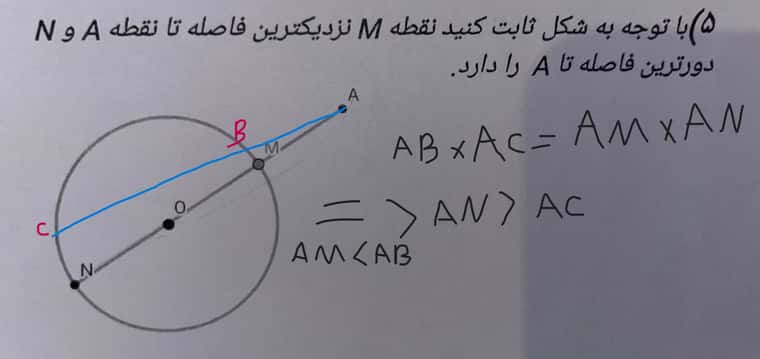
این رابطه که میدونیم همیشه بر قراره و توی فصل 1 یازدهم اثبات هم میشه، طبق اثباتی که اول همین پیام کردم AB بزرگتر از AM هست. پس بدیهیه که AN بزرگتر از َAC هست. -
سلام، این روش ها برای اثبات به ذهنم اومد:
برای اثبات اینکه نقطه M نزدیک ترین فاصله هست به شکل زیر عمل میکنیم:

خط مماس بر دایره که از نقطه M میگذره رو رسم میکنیم، میدونیم این خط بر AN عموده، حالا اینجا میایم ادعا میکنیم که این نقطه نزدیک ترین نقطه هست، برای اثبات این موضوع میایم نقطه C رو که یه نقطه دلخواه یه جای دیگه دایره هست فرض میکنیم، میگیم چون AB وتره مطابق شکل، پس از AM بزرگتره، پس AB + یه چیز دیگه که اینجا CB هست هم از AM بزرگتره، پس AC از AM بزرگتره، در نتیجه AM کوچیترین فاصله هست.
.
.
برای اثبات دورترین بودن N هم میشه از راه حل زیر رفت:

فکر کنم همه چی مشخصه، ولی خب، مطابق شکل خطی رو به دایره که از نقطه M میگذره مماس میکنیم، C یه نقطه فرضی دیگه هست روی دایره، C رو به M وصل میکنیم تا مثلث CNM ساخته بشه، با زاویره C1، خب اینجا C1، نود درجه هست، چون زاویه محاطی هست و کمان رو به روش 180 درجست... C اینجا تشکیل شده از C1 که نود درجه هست و یه زاویه دیگه به اسم C2، پس در نتیجه زاویه C بزرگتر از 90 هست پس درنتیجه بزرگترین زاویه مثلث ACN هست، طبق قضیه ضلع و زاویه برتر، AN بزرگتر از AC هست، پس N دورترین نقطه از A روی دایره هست.
.
.
هرچند روش دومی هم به ذهنم رسید برای اثبات دومی، میشه از روابط طولی استفاده کرد:

این رابطه که میدونیم همیشه بر قراره و توی فصل 1 یازدهم اثبات هم میشه، طبق اثباتی که اول همین پیام کردم AB بزرگتر از AM هست. پس بدیهیه که AN بزرگتر از َAC هست.