معادله نامعادله ی قلم چی
-
سلام. برای حل این تست خیلی راحت ترید که تعیین علامت سریع بلد باشید، احتمال بالا هم بلدید، همون روش تک سطری که بعدش میایم از بیشترین توانا کمک میگیریم تا علامت اول رو تعیین کنیم، بعدش هم یکی در میون عوض میکنیم مگر اینکه ریشه مضاعف باشه، اگر نمیدونید بگید توضیح بدم.
خب اینجا از رو منفی سه پریده، یعنی منفی سه ریشه مضاعفه، یک ریشه عادی. پرانتز هامون رو میبینیم، یه پرانتز درجه دو هست(چون توان دو داره) و خب مضاعفه، یکیش درجه یکه و ریشه مضاعف نیست. پس می فهمیم که ریشه منفی سه مربوط به پرانتز توان دو دارمونه و ریشه یک مربوط به پرانتز درجه یک. یعنی این دو عدد به ترتیب پرانتزامون رو صفر میکنن:
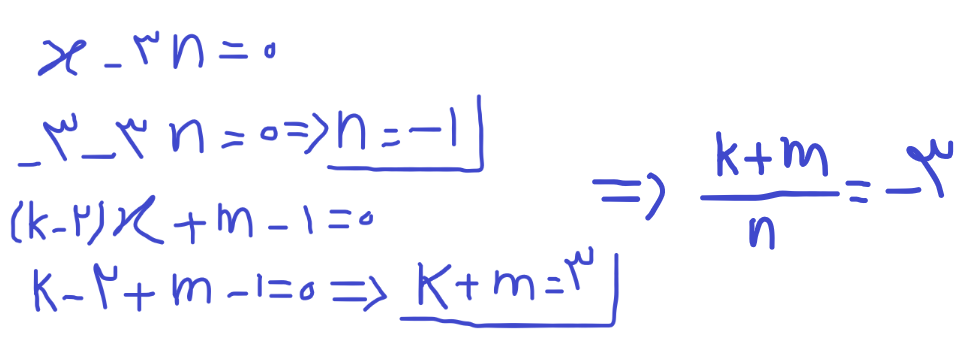
اینجا همونطور که میبینید ما مقدار دقیق کا و ام رو به دست نیاوردیم، ولی نیازی هم نبود، چون ما مقدار کا + ام رو میخواستیم که به دست آوردم. -
سلام. برای حل این تست خیلی راحت ترید که تعیین علامت سریع بلد باشید، احتمال بالا هم بلدید، همون روش تک سطری که بعدش میایم از بیشترین توانا کمک میگیریم تا علامت اول رو تعیین کنیم، بعدش هم یکی در میون عوض میکنیم مگر اینکه ریشه مضاعف باشه، اگر نمیدونید بگید توضیح بدم.
خب اینجا از رو منفی سه پریده، یعنی منفی سه ریشه مضاعفه، یک ریشه عادی. پرانتز هامون رو میبینیم، یه پرانتز درجه دو هست(چون توان دو داره) و خب مضاعفه، یکیش درجه یکه و ریشه مضاعف نیست. پس می فهمیم که ریشه منفی سه مربوط به پرانتز توان دو دارمونه و ریشه یک مربوط به پرانتز درجه یک. یعنی این دو عدد به ترتیب پرانتزامون رو صفر میکنن:
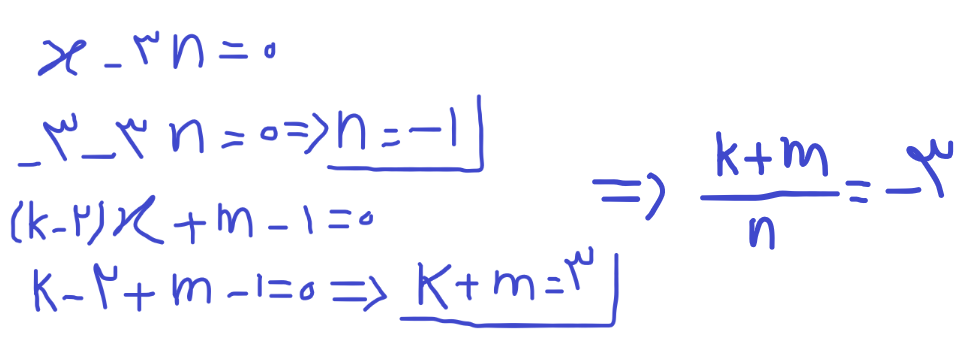
اینجا همونطور که میبینید ما مقدار دقیق کا و ام رو به دست نیاوردیم، ولی نیازی هم نبود، چون ما مقدار کا + ام رو میخواستیم که به دست آوردم.@Comrade_Bayat در معادله نامعادله ی قلم چی گفته است:
سلام. برای حل این تست خیلی راحت ترید که تعیین علامت سریع بلد باشید، احتمال بالا هم بلدید، همون روش تک سطری که بعدش میایم از بیشترین توانا کمک میگیریم تا علامت اول رو تعیین کنیم، بعدش هم یکی در میون عوض میکنیم مگر اینکه ریشه مضاعف باشه، اگر نمیدونید بگید توضیح بدم.
ممنون میشم رو همین مثال توضیح بدین
خب اینجا از رو منفی سه پریده، یعنی منفی سه ریشه مضاعفه، یک ریشه عادی. پرانتز هامون رو میبینیم، یه پرانتز درجه دو هست(چون توان دو داره) و خب مضاعفه، یکیش درجه یکه و ریشه مضاعف نیست. پس می فهمیم که ریشه منفی سه مربوط به پرانتز توان دو دارمونه و ریشه یک مربوط به پرانتز درجه یک.
چطور تشخیص میدین هر ریشه برای کدوم بخش هست؟
و این که 3 رو چون دو طرفش هم علامته میگید ریشه مضاعفه؟ -
@Comrade_Bayat در معادله نامعادله ی قلم چی گفته است:
سلام. برای حل این تست خیلی راحت ترید که تعیین علامت سریع بلد باشید، احتمال بالا هم بلدید، همون روش تک سطری که بعدش میایم از بیشترین توانا کمک میگیریم تا علامت اول رو تعیین کنیم، بعدش هم یکی در میون عوض میکنیم مگر اینکه ریشه مضاعف باشه، اگر نمیدونید بگید توضیح بدم.
ممنون میشم رو همین مثال توضیح بدین
خب اینجا از رو منفی سه پریده، یعنی منفی سه ریشه مضاعفه، یک ریشه عادی. پرانتز هامون رو میبینیم، یه پرانتز درجه دو هست(چون توان دو داره) و خب مضاعفه، یکیش درجه یکه و ریشه مضاعف نیست. پس می فهمیم که ریشه منفی سه مربوط به پرانتز توان دو دارمونه و ریشه یک مربوط به پرانتز درجه یک.
چطور تشخیص میدین هر ریشه برای کدوم بخش هست؟
و این که 3 رو چون دو طرفش هم علامته میگید ریشه مضاعفه؟Hg L 0 سلام
خب رو همین که نمیشه، باید مشخص باشه، مثلا این عبارت رو نگاه کنید:

این عبارتمونه، خب بعضیا اول میان ساده میکنن، ولی من از این کار زیاد خوشم نمیاد، در عوض میام ریشه های هر پرانتز رو حساب میکنم و مینویسم، نتیجه شمردنم شده اون نوشته سمت راست، ریشه سه چهار بار اومده، ریشه یک یک بار، و یه صفر هم گذاشتم جلوش یعنی این ریشه عبارت رو صفر میکنه، ریشه های دیگه چون توی مخرج هم هستن، عبارت رو صفر نمیکنن و تعریف نشده میشه، و همینطور تا آخر.(دقت کنید وقتی مثل پرانتز اول ریشه مضاعف داریم دو بار حسابش میکنم، یا اگه توان سه باشه سه بار، یا چهار، چهار بار و ...، برای درک بهتر میتونید پرانتزا رو توی ذهنتون باز کنید، یعنی ایکس منهای سه ضرب در ایکس منهای سه، هر کدومشون یه ریشه داره!)
بعدش جدول تعیین علامت رو کشیدن، من خودم توی جدول کشیدن برای تعریف نشده ها، یعنی همونا که مخرج رو صفر میکنن دو تا خط میزارم، بعضی ها هم یه خط میکشن روش مینویسن ت ن(تعریف نشده)، روش های مختلفی هست که سلیقه ایه.
هرچند اگر اینجا ساده کرده بودید و با روش من نرفتید، باید ببینید کدوم ریشه، مخرج عبارت اولیه رو صفر میکنه، صرفا عبارت ساده شده ملاک نیست.
بعدش هم میام توی هر عبارت میبینم ضریب بزرگترین درجه چیه، عبارت اول ینی پرانتز ایکس منهای سه به توان دو، بزرگترین درجه متغیرش اینجا ایکسه، ضریب ایکس علامتش مثبته، مینویسم، بعدی ضریب ایکس دو مثبته، مینویسم، بعدی یعنی منفی یکه، در اصل اونم متغییر داره، منفی یک اینجا منفی یک ضرب در ایکس به توان منهای صفره! یعنی همون منفی یک، پس خودش بزرگترین درجست! منفی رو مینویسم، ضریب ایکس دوی عبارت بعدی هم مثبته، سر هم میشه سه تا مثبت در یک منفی که منفیه! توی جدولم از راست شروع به گذاشتن علامت میکنم، منفی اولیشه، چون سه تعداد ریشه هاش زوجه یا اصطلاحا مضاعفه، از روش میپرم و باز منفی میزارم، بعدش بعد یک علامت رو عوض میکنم چون مضاعف نیست، علامت رو بعد منفی دو هم عوض میکنم چون مضاعف نیست، بعدی هم همینطور. به این میگن تعیین علامت سریع.
خب برگردیم به مسئله.Hg L 0 در معادله نامعادله ی قلم چی گفته است:
و این که 3 رو چون دو طرفش هم علامته میگید ریشه مضاعفه؟
خب طبق روشی که بالا گفتم فکر کنم فهمیده باشید، چون از روی منفی سه پریدیم و علامت عوض نکردیم مضاعفه! بیایم روی پرانتز ها، ما یه ریشه غیر مضاعف یعنی یک داریم، یکی هم مضاعف، یک پرانتز درجه یک(پرانتز اول) و یکی درجه دو داریم. اینجا همون اول مشخص میشه ریشه منفی سه برای پرانتز دومه و یک برای پرانتز اول، ولی میشه دقیق تر نگاه کرد، اینجا ما دو حالت ریشه داریم، اولیش این که ریشه هر دو پرانتز با هم برابر باشه، دومی اینکه پرانتز اولیه یه ریشه ای بده، و دومی هم یه رشه دیگه، البته اگه عبارت دوممون یه درجه دو با فرمول عادی بود، یعنی حالت آ ایکس دو + ب ایکس + سی میشد حالت های دیگه ای هم در نظر گرفت، مثل حالتی که پرانتز اول یه ریشه بده، دومی دو ریشه متفاوت از هم که با اولی برابر هم نیستن، یا پرانتز دوم دو ریشه بده که یکیش با اولی مساویه، یا پرانتز دوم کلا ریشه ای نداشته باشه و دلتاش منفی باشه. که خب ما چون دو تا ریشه داریم حالت دوم که نمیشه پس همون اولیه هست و مشخص میشه کدوم ریشه برای کدوم پرانتزه.
-
Hg L 0 سلام
خب رو همین که نمیشه، باید مشخص باشه، مثلا این عبارت رو نگاه کنید:

این عبارتمونه، خب بعضیا اول میان ساده میکنن، ولی من از این کار زیاد خوشم نمیاد، در عوض میام ریشه های هر پرانتز رو حساب میکنم و مینویسم، نتیجه شمردنم شده اون نوشته سمت راست، ریشه سه چهار بار اومده، ریشه یک یک بار، و یه صفر هم گذاشتم جلوش یعنی این ریشه عبارت رو صفر میکنه، ریشه های دیگه چون توی مخرج هم هستن، عبارت رو صفر نمیکنن و تعریف نشده میشه، و همینطور تا آخر.(دقت کنید وقتی مثل پرانتز اول ریشه مضاعف داریم دو بار حسابش میکنم، یا اگه توان سه باشه سه بار، یا چهار، چهار بار و ...، برای درک بهتر میتونید پرانتزا رو توی ذهنتون باز کنید، یعنی ایکس منهای سه ضرب در ایکس منهای سه، هر کدومشون یه ریشه داره!)
بعدش جدول تعیین علامت رو کشیدن، من خودم توی جدول کشیدن برای تعریف نشده ها، یعنی همونا که مخرج رو صفر میکنن دو تا خط میزارم، بعضی ها هم یه خط میکشن روش مینویسن ت ن(تعریف نشده)، روش های مختلفی هست که سلیقه ایه.
هرچند اگر اینجا ساده کرده بودید و با روش من نرفتید، باید ببینید کدوم ریشه، مخرج عبارت اولیه رو صفر میکنه، صرفا عبارت ساده شده ملاک نیست.
بعدش هم میام توی هر عبارت میبینم ضریب بزرگترین درجه چیه، عبارت اول ینی پرانتز ایکس منهای سه به توان دو، بزرگترین درجه متغیرش اینجا ایکسه، ضریب ایکس علامتش مثبته، مینویسم، بعدی ضریب ایکس دو مثبته، مینویسم، بعدی یعنی منفی یکه، در اصل اونم متغییر داره، منفی یک اینجا منفی یک ضرب در ایکس به توان منهای صفره! یعنی همون منفی یک، پس خودش بزرگترین درجست! منفی رو مینویسم، ضریب ایکس دوی عبارت بعدی هم مثبته، سر هم میشه سه تا مثبت در یک منفی که منفیه! توی جدولم از راست شروع به گذاشتن علامت میکنم، منفی اولیشه، چون سه تعداد ریشه هاش زوجه یا اصطلاحا مضاعفه، از روش میپرم و باز منفی میزارم، بعدش بعد یک علامت رو عوض میکنم چون مضاعف نیست، علامت رو بعد منفی دو هم عوض میکنم چون مضاعف نیست، بعدی هم همینطور. به این میگن تعیین علامت سریع.
خب برگردیم به مسئله.Hg L 0 در معادله نامعادله ی قلم چی گفته است:
و این که 3 رو چون دو طرفش هم علامته میگید ریشه مضاعفه؟
خب طبق روشی که بالا گفتم فکر کنم فهمیده باشید، چون از روی منفی سه پریدیم و علامت عوض نکردیم مضاعفه! بیایم روی پرانتز ها، ما یه ریشه غیر مضاعف یعنی یک داریم، یکی هم مضاعف، یک پرانتز درجه یک(پرانتز اول) و یکی درجه دو داریم. اینجا همون اول مشخص میشه ریشه منفی سه برای پرانتز دومه و یک برای پرانتز اول، ولی میشه دقیق تر نگاه کرد، اینجا ما دو حالت ریشه داریم، اولیش این که ریشه هر دو پرانتز با هم برابر باشه، دومی اینکه پرانتز اولیه یه ریشه ای بده، و دومی هم یه رشه دیگه، البته اگه عبارت دوممون یه درجه دو با فرمول عادی بود، یعنی حالت آ ایکس دو + ب ایکس + سی میشد حالت های دیگه ای هم در نظر گرفت، مثل حالتی که پرانتز اول یه ریشه بده، دومی دو ریشه متفاوت از هم که با اولی برابر هم نیستن، یا پرانتز دوم دو ریشه بده که یکیش با اولی مساویه، یا پرانتز دوم کلا ریشه ای نداشته باشه و دلتاش منفی باشه. که خب ما چون دو تا ریشه داریم حالت دوم که نمیشه پس همون اولیه هست و مشخص میشه کدوم ریشه برای کدوم پرانتزه.












