سوال
-
سلام
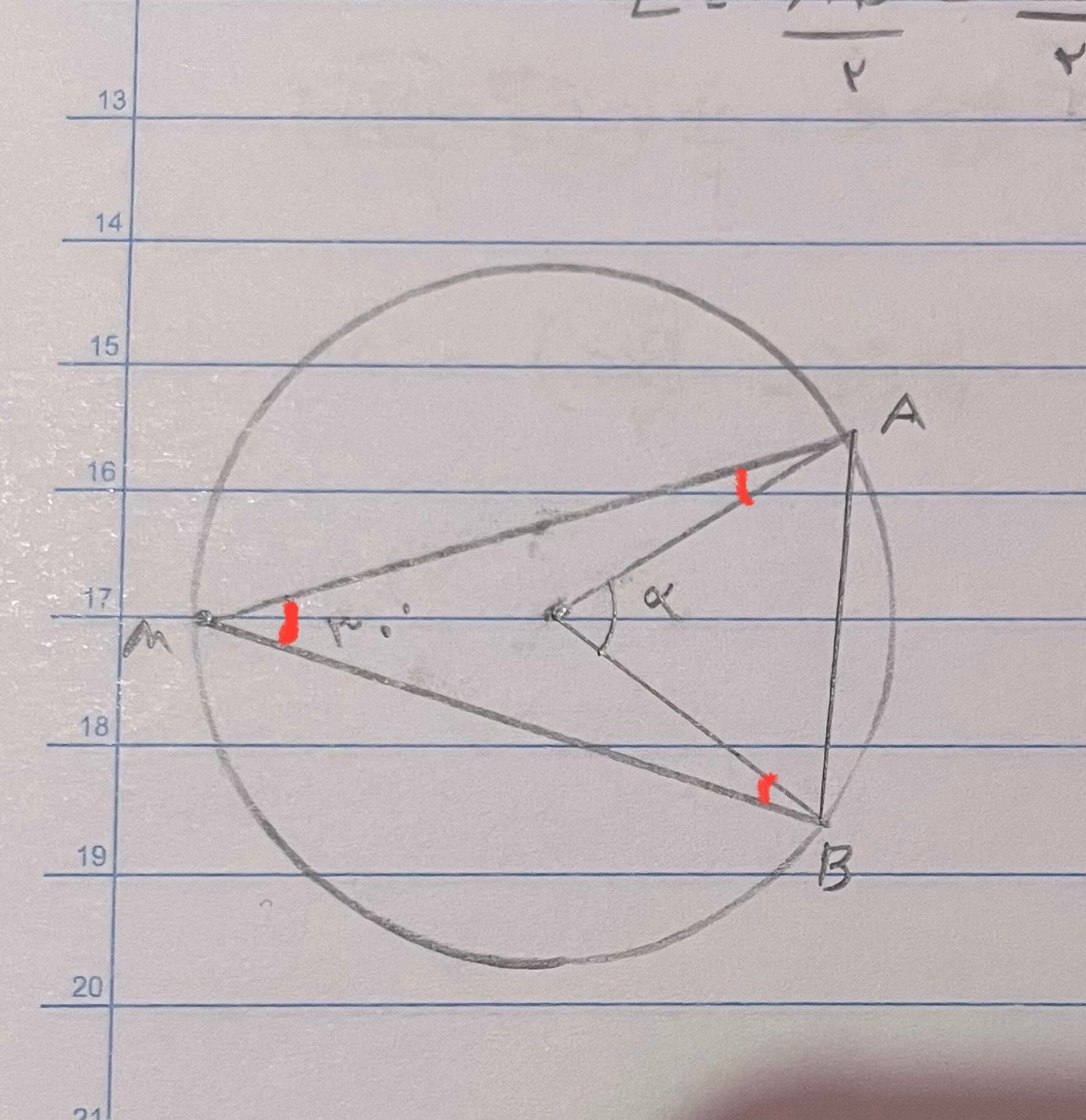
دایره ای به شعاع ۴ و نقطه m به فاصله ۱ واحد از مرکز دایره مفروض است.چند وتر میتوان رسم کرد که طولشان ۲ باشد و از m بگذرد -
سلام
دایره ای به شعاع ۴ و نقطه m به فاصله ۱ واحد از مرکز دایره مفروض است.چند وتر میتوان رسم کرد که طولشان ۲ باشد و از m بگذردmohammad javad Khoshsolat سلام .هیچ وتری نمیشه با این طول رسم کرد. کلا در نظر بگیرید از هر نقطه ای یا میشه 0 یا 1 یا 2 وتر با طول خاص داخل یه دایره کشید که از نقطه مورد نظر بگذره .
اگر وتری که ازتون خواستن اندازه قطر بود و اندازه دو برابر رادیکال شعاع به توان 2 منهای فاصله نقطه از مرکز به توان دو بود میشه 1 وتر اگر بین این دو عدد بود میشه 2 وتر و خارج این بازه میشه 0 وتر .
توی این سوال شما میشه از 2 رادیکال13 که میشه حدود 7.1 تا 8 چون 2 توی این بازه نیست پس وتری با این طول از m نمیگذره -
انصافا نفهمیدم چی شد ولی خیلی ممنون که پاسخ دادید
-
انصافا نفهمیدم چی شد ولی خیلی ممنون که پاسخ دادید
mohammad javad Khoshsolat در سوال گفته است:
انصافا نفهمیدم چی شد ولی خیلی ممنون که پاسخ دادید
سلام
اندازه کوچکترین وتری که میشه از یه نقطه درون دایره رسم کرد از فرمول مقابل حساب میشه:
\(\sqrt{R^2-d^2}\)2
(R=شعاع و d=فاصله نقطه از مرکز) اثباتش هم از طریق فیثاغورس هست
و میدونیم که بزرگترین وتری که میشه از یه نقطه درون دایره رسم کرد وتریه که از اون نقطه و مرکز بگذره یعنی همون قطر دایره
حالا اگر طول وتر مطرح شده تو سوال برابر با کوچکترین وتر(\(\sqrt{R^2-d^2}\)2) یا بزرگترین وتر(قطر) باشه فقط 1 وتر میشه از نقطه ی mرسم کرد
اما اگر قطر>طول وتر مطرح شده در سوال>\(\sqrt{R^2-d^2}\)2
باشه 2 وتر میشه از نقطه mرسم کرد(اگه خواستی بهتر بفهمی یه دایره رسم کن یه نقطه توش انتخاب کن و از اون نقطه یه خط موازی قطر دایره رسم کن میبینی که قطر و خطی که کشیدی تو 4 نقطه دایره رو قطع میکنن که دو تا وتر هم اندازه میشه بینشون رسم کرد)
و حالت سوم اینه که طول وترمطرح شده هیچ کدوم از شرایط بالا رو نداشته باشه یعنی یا از قطر بزرگتر باشه و یا از کوچکترین وتر هم کمتر باشه
الان تو این سوال طول وتر که گفته شده 2 هست که از\(\sqrt{15}\)2=\(\sqrt{4^2-1^2}\)2 یعنی کوچکترین وتر هم کوچک تره پس هیچ وتری با طول 2 نمیشه از نقطه mرسم کرد
دیگه داداش اگه خودتم بخوای نمیتونی نفهمی با این طومار توضیحات
-- -- -- -- -- -- --Death
Life =∫ Happiness/Time
-- -- -- -- -- -- -- --Birth -
mohammad javad Khoshsolat در سوال گفته است:
انصافا نفهمیدم چی شد ولی خیلی ممنون که پاسخ دادید
سلام
اندازه کوچکترین وتری که میشه از یه نقطه درون دایره رسم کرد از فرمول مقابل حساب میشه:
\(\sqrt{R^2-d^2}\)2
(R=شعاع و d=فاصله نقطه از مرکز) اثباتش هم از طریق فیثاغورس هست
و میدونیم که بزرگترین وتری که میشه از یه نقطه درون دایره رسم کرد وتریه که از اون نقطه و مرکز بگذره یعنی همون قطر دایره
حالا اگر طول وتر مطرح شده تو سوال برابر با کوچکترین وتر(\(\sqrt{R^2-d^2}\)2) یا بزرگترین وتر(قطر) باشه فقط 1 وتر میشه از نقطه ی mرسم کرد
اما اگر قطر>طول وتر مطرح شده در سوال>\(\sqrt{R^2-d^2}\)2
باشه 2 وتر میشه از نقطه mرسم کرد(اگه خواستی بهتر بفهمی یه دایره رسم کن یه نقطه توش انتخاب کن و از اون نقطه یه خط موازی قطر دایره رسم کن میبینی که قطر و خطی که کشیدی تو 4 نقطه دایره رو قطع میکنن که دو تا وتر هم اندازه میشه بینشون رسم کرد)
و حالت سوم اینه که طول وترمطرح شده هیچ کدوم از شرایط بالا رو نداشته باشه یعنی یا از قطر بزرگتر باشه و یا از کوچکترین وتر هم کمتر باشه
الان تو این سوال طول وتر که گفته شده 2 هست که از\(\sqrt{15}\)2=\(\sqrt{4^2-1^2}\)2 یعنی کوچکترین وتر هم کوچک تره پس هیچ وتری با طول 2 نمیشه از نقطه mرسم کرد
دیگه داداش اگه خودتم بخوای نمیتونی نفهمی با این طومار توضیحات -
Reza.Tah دم شما گرم
داشتم عکس توضیحش رو میذاشتم که شما گفتی دیگه.فقط اون خط آخر رو ادیت کن 4به توان 2 هستش.شعاع چهار هست درواقع -
mohammad javad Khoshsolat در سوال گفته است:
انصافا نفهمیدم چی شد ولی خیلی ممنون که پاسخ دادید
سلام
اندازه کوچکترین وتری که میشه از یه نقطه درون دایره رسم کرد از فرمول مقابل حساب میشه:
\(\sqrt{R^2-d^2}\)2
(R=شعاع و d=فاصله نقطه از مرکز) اثباتش هم از طریق فیثاغورس هست
و میدونیم که بزرگترین وتری که میشه از یه نقطه درون دایره رسم کرد وتریه که از اون نقطه و مرکز بگذره یعنی همون قطر دایره
حالا اگر طول وتر مطرح شده تو سوال برابر با کوچکترین وتر(\(\sqrt{R^2-d^2}\)2) یا بزرگترین وتر(قطر) باشه فقط 1 وتر میشه از نقطه ی mرسم کرد
اما اگر قطر>طول وتر مطرح شده در سوال>\(\sqrt{R^2-d^2}\)2
باشه 2 وتر میشه از نقطه mرسم کرد(اگه خواستی بهتر بفهمی یه دایره رسم کن یه نقطه توش انتخاب کن و از اون نقطه یه خط موازی قطر دایره رسم کن میبینی که قطر و خطی که کشیدی تو 4 نقطه دایره رو قطع میکنن که دو تا وتر هم اندازه میشه بینشون رسم کرد)
و حالت سوم اینه که طول وترمطرح شده هیچ کدوم از شرایط بالا رو نداشته باشه یعنی یا از قطر بزرگتر باشه و یا از کوچکترین وتر هم کمتر باشه
الان تو این سوال طول وتر که گفته شده 2 هست که از\(\sqrt{15}\)2=\(\sqrt{4^2-1^2}\)2 یعنی کوچکترین وتر هم کوچک تره پس هیچ وتری با طول 2 نمیشه از نقطه mرسم کرد
دیگه داداش اگه خودتم بخوای نمیتونی نفهمی با این طومار توضیحاتReza.Tah
خیلی ممنون من به اون رادیکال ۱۳ شک کردم
