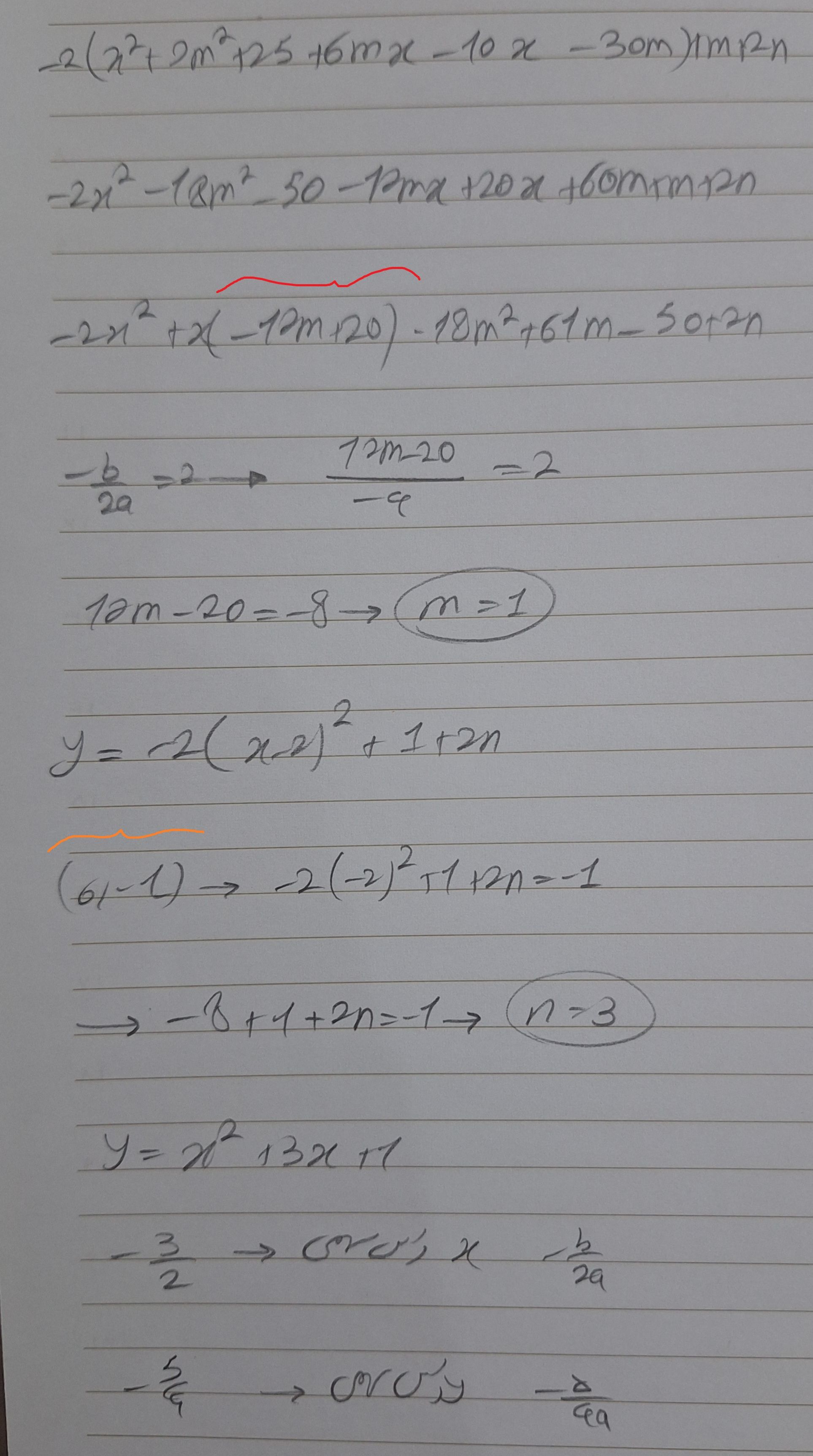هم توضیح هم محاسبات
-
تست اول: خب گفته این راس روی نیمساز ناحیه دوم واقع هست، یعنی نیمساز ناحیه دوم رو قطع کرده، نیمساز ناحیه دوم چیه؟ y=-x
پس مساوی هم قرار میدیم: (این نکته رو هم در نظر داشته باشید طول راس سهمی منفی بی به روی دو آ هست)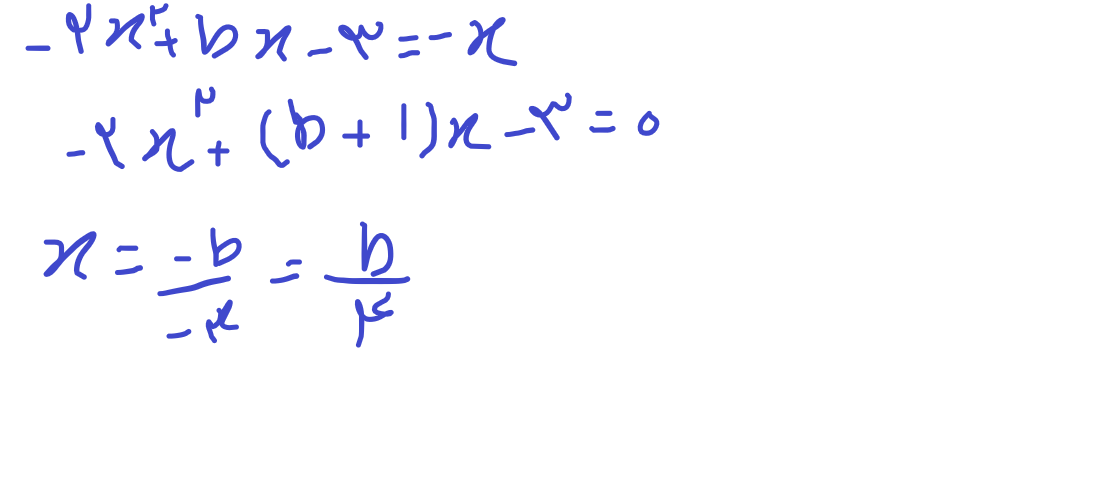
خب اینجا دو راه داریم، یا جایگزاری ایکسمون و حل تا آخر، یا جایگزاری گزینه ها!
اگر حل کنیم به این میرسیم که ایکس میتونه چهار باشه یا منفی شش! اگرم جایگزاری کنیم میبینیم هر دوی این ها میشن! بستگی به دید طراح داره که گزینه دو رو بگیره یا سه! طراح دقیق نگفته راس حتما باید توی ناحیه دو باشه یا ناحیه چهار هم قبوله... چون نیمساز ناحیه دوم یه خطه که از ناحیه چهار هم رد میشه، اگه بگیم میتونه ناحیه چهار هم باشه میشه گزینه سه، اگر نه گزینه دو، چون طبق خط آخر که نوشتم بی باید منفی باشه تا توی ناحیه دوم بیفته.
برای اینکه بهتر متوجه بشید چی میگم نمودار ها رو رسم میکنم:
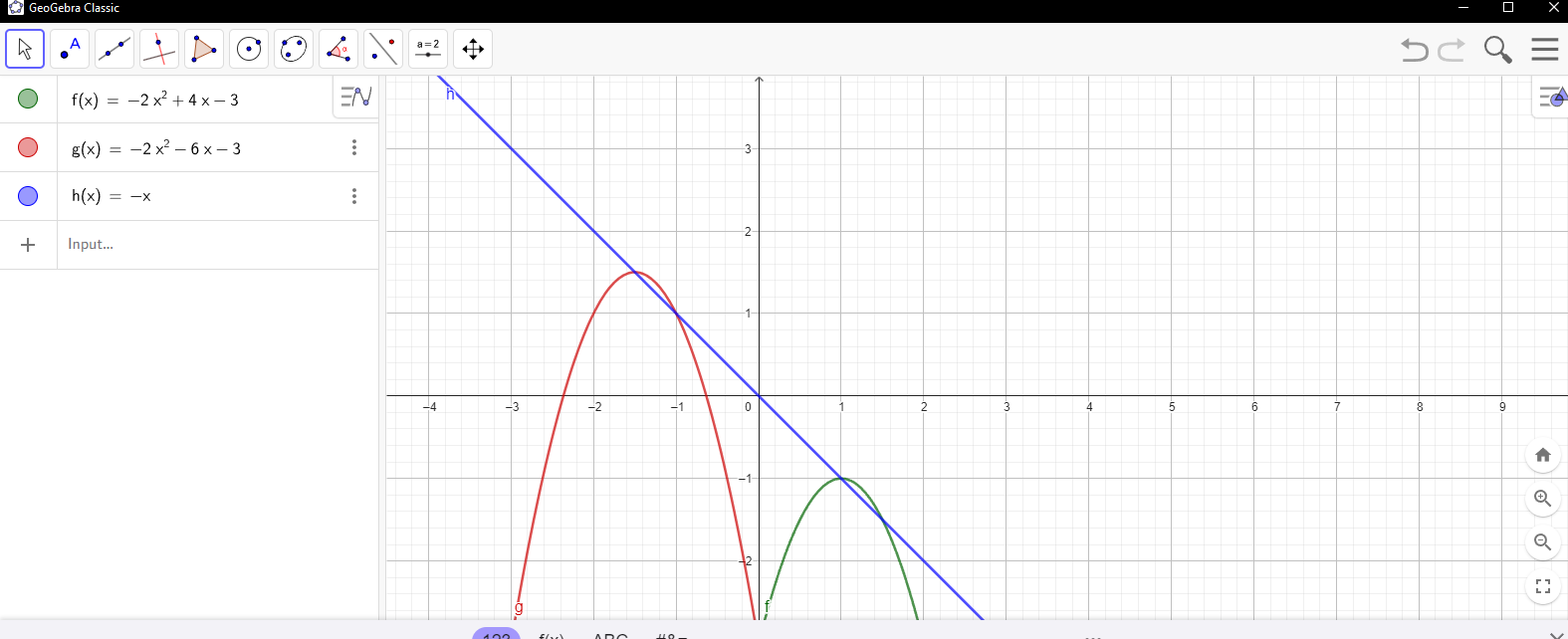
هر چند در نهایت بنظرم گزینه دو منطقی تره و جواب درست تریه -
-
تست اول: خب گفته این راس روی نیمساز ناحیه دوم واقع هست، یعنی نیمساز ناحیه دوم رو قطع کرده، نیمساز ناحیه دوم چیه؟ y=-x
پس مساوی هم قرار میدیم: (این نکته رو هم در نظر داشته باشید طول راس سهمی منفی بی به روی دو آ هست)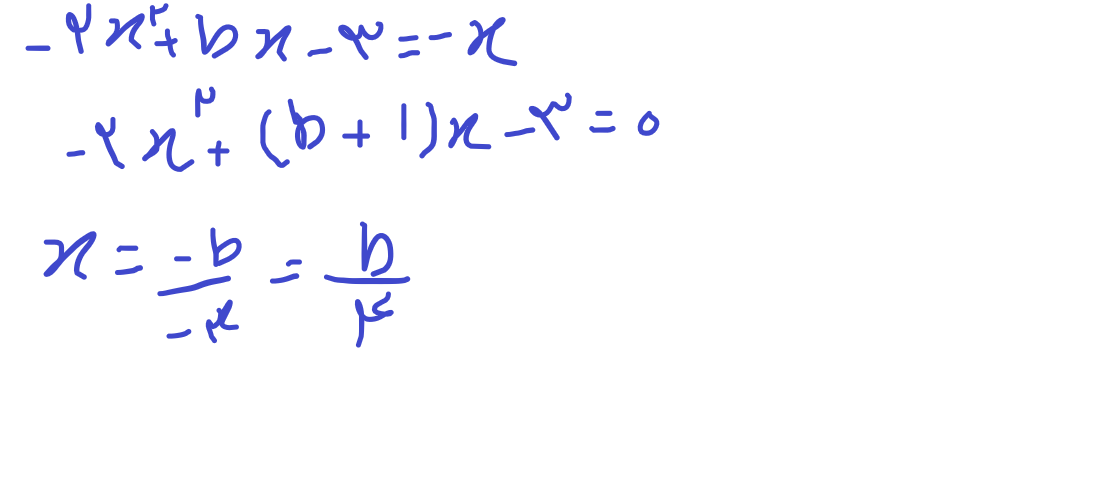
خب اینجا دو راه داریم، یا جایگزاری ایکسمون و حل تا آخر، یا جایگزاری گزینه ها!
اگر حل کنیم به این میرسیم که ایکس میتونه چهار باشه یا منفی شش! اگرم جایگزاری کنیم میبینیم هر دوی این ها میشن! بستگی به دید طراح داره که گزینه دو رو بگیره یا سه! طراح دقیق نگفته راس حتما باید توی ناحیه دو باشه یا ناحیه چهار هم قبوله... چون نیمساز ناحیه دوم یه خطه که از ناحیه چهار هم رد میشه، اگه بگیم میتونه ناحیه چهار هم باشه میشه گزینه سه، اگر نه گزینه دو، چون طبق خط آخر که نوشتم بی باید منفی باشه تا توی ناحیه دوم بیفته.
برای اینکه بهتر متوجه بشید چی میگم نمودار ها رو رسم میکنم:

هر چند در نهایت بنظرم گزینه دو منطقی تره و جواب درست تریه -
تست اول: خب گفته این راس روی نیمساز ناحیه دوم واقع هست، یعنی نیمساز ناحیه دوم رو قطع کرده، نیمساز ناحیه دوم چیه؟ y=-x
پس مساوی هم قرار میدیم: (این نکته رو هم در نظر داشته باشید طول راس سهمی منفی بی به روی دو آ هست)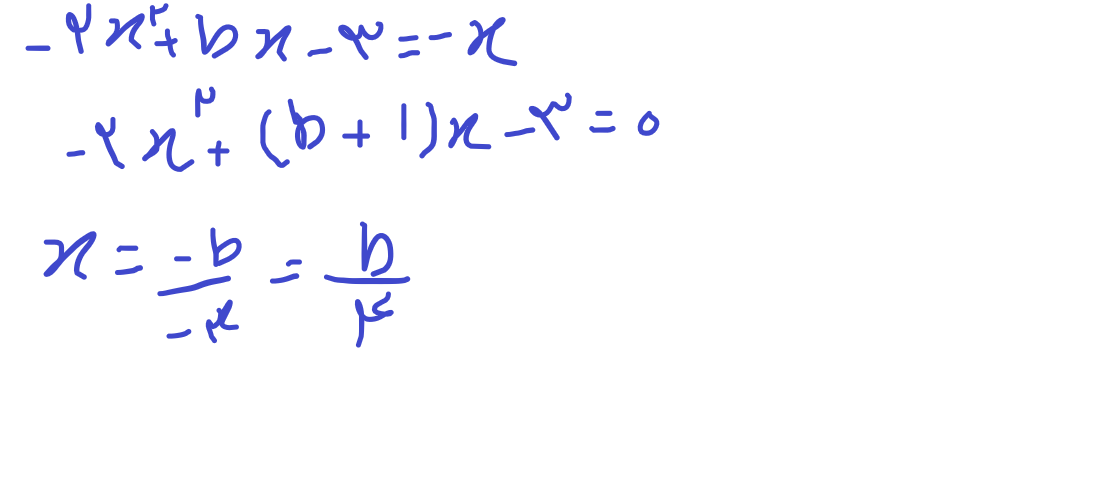
خب اینجا دو راه داریم، یا جایگزاری ایکسمون و حل تا آخر، یا جایگزاری گزینه ها!
اگر حل کنیم به این میرسیم که ایکس میتونه چهار باشه یا منفی شش! اگرم جایگزاری کنیم میبینیم هر دوی این ها میشن! بستگی به دید طراح داره که گزینه دو رو بگیره یا سه! طراح دقیق نگفته راس حتما باید توی ناحیه دو باشه یا ناحیه چهار هم قبوله... چون نیمساز ناحیه دوم یه خطه که از ناحیه چهار هم رد میشه، اگه بگیم میتونه ناحیه چهار هم باشه میشه گزینه سه، اگر نه گزینه دو، چون طبق خط آخر که نوشتم بی باید منفی باشه تا توی ناحیه دوم بیفته.
برای اینکه بهتر متوجه بشید چی میگم نمودار ها رو رسم میکنم:

هر چند در نهایت بنظرم گزینه دو منطقی تره و جواب درست تریه -
Hg L 0
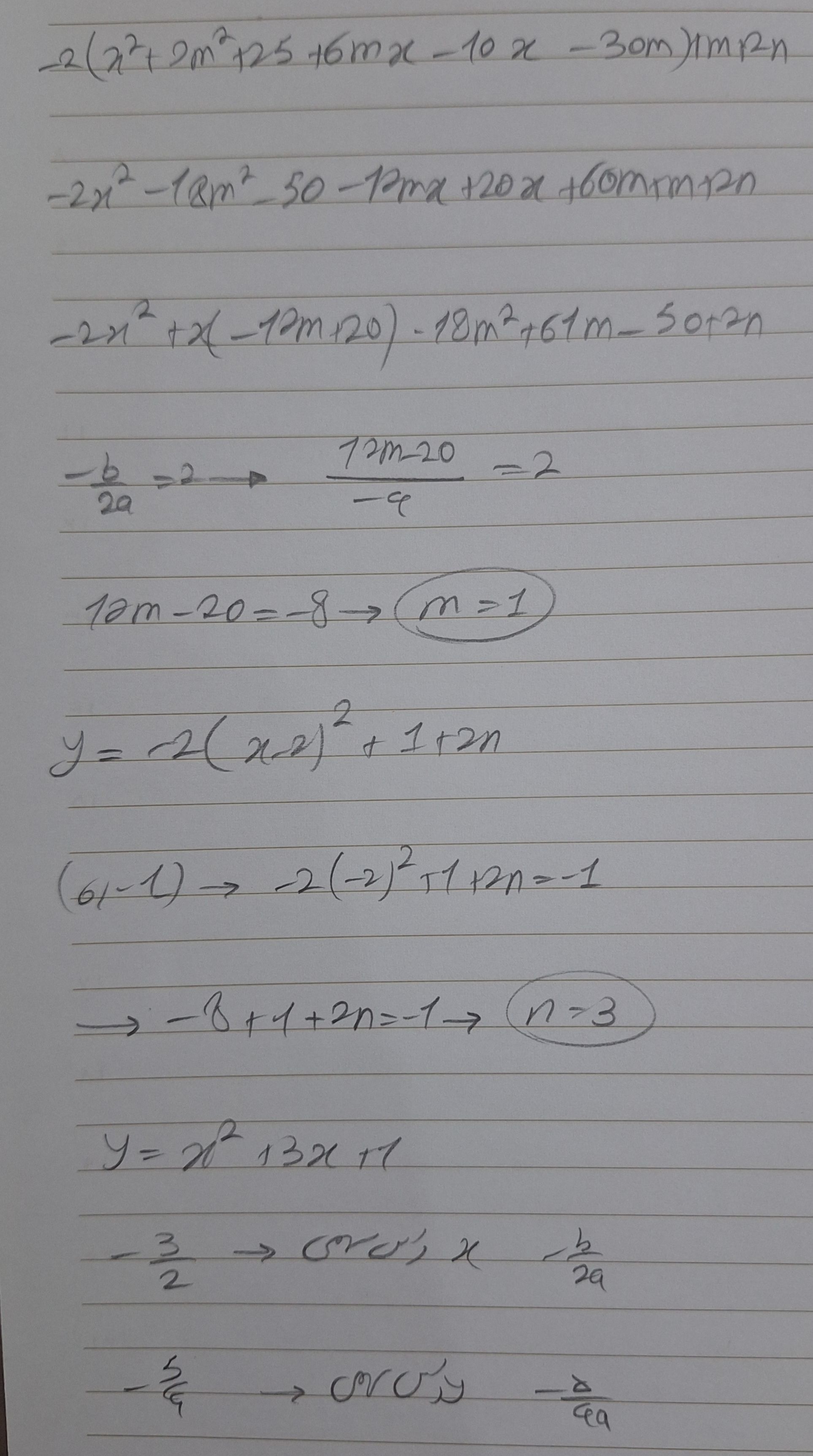
این دومی
توضیح خاصی هم نداره راس سهمی داخل شکل مشخصه و اینکه عرض از مبدا رو هم داریم هر دو به دست میان -
تست اول: خب گفته این راس روی نیمساز ناحیه دوم واقع هست، یعنی نیمساز ناحیه دوم رو قطع کرده، نیمساز ناحیه دوم چیه؟ y=-x
پس مساوی هم قرار میدیم: (این نکته رو هم در نظر داشته باشید طول راس سهمی منفی بی به روی دو آ هست)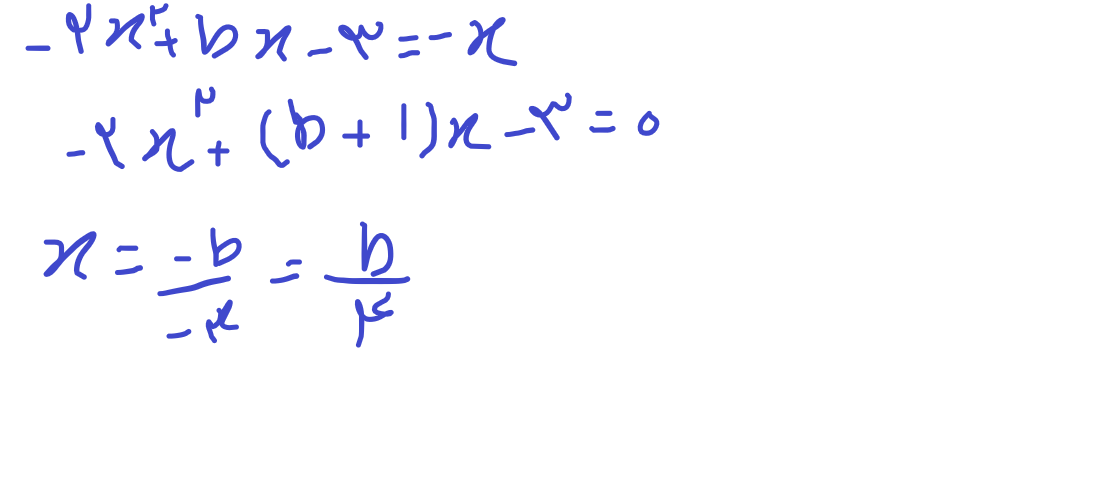
خب اینجا دو راه داریم، یا جایگزاری ایکسمون و حل تا آخر، یا جایگزاری گزینه ها!
اگر حل کنیم به این میرسیم که ایکس میتونه چهار باشه یا منفی شش! اگرم جایگزاری کنیم میبینیم هر دوی این ها میشن! بستگی به دید طراح داره که گزینه دو رو بگیره یا سه! طراح دقیق نگفته راس حتما باید توی ناحیه دو باشه یا ناحیه چهار هم قبوله... چون نیمساز ناحیه دوم یه خطه که از ناحیه چهار هم رد میشه، اگه بگیم میتونه ناحیه چهار هم باشه میشه گزینه سه، اگر نه گزینه دو، چون طبق خط آخر که نوشتم بی باید منفی باشه تا توی ناحیه دوم بیفته.
برای اینکه بهتر متوجه بشید چی میگم نمودار ها رو رسم میکنم:

هر چند در نهایت بنظرم گزینه دو منطقی تره و جواب درست تریه -
@Comrade_Bayat خیلی ممنونم
فقط سوالم اینه وقتی میگه نمیساز راس رو قطع کرده چطور میایم و دو معادله رو مساوی هم قرار میدیم؟
توضیح بدین علتش رو لطفاHg L 0 خواهش میکنم
ببینید وقتی دو تابع هم دیگه رو قطع کردن، یعنی یک نقطه مساوی دارن، توی اون نقطه y ها برابر و x ها هم برابرن، پس من میام برای یافتن ایکس y ها که در اصل همون ضابطه تابع هستن مساوی هم قرار میدم تا ایکس مشترکشون پیدا بشه! در این صورت اگر ایکس یا ایکس های به دست اومده رو توی هر کدوم از ضابطه ها قرار بدیم y مشترک هم پیدا میشه. -
Hako برای اندروید هم اگه بخواین
Math ally graphics classic -
Hg L 0 خواهش میکنم
ببینید وقتی دو تابع هم دیگه رو قطع کردن، یعنی یک نقطه مساوی دارن، توی اون نقطه y ها برابر و x ها هم برابرن، پس من میام برای یافتن ایکس y ها که در اصل همون ضابطه تابع هستن مساوی هم قرار میدم تا ایکس مشترکشون پیدا بشه! در این صورت اگر ایکس یا ایکس های به دست اومده رو توی هر کدوم از ضابطه ها قرار بدیم y مشترک هم پیدا میشه. -
 H Hg L 0 marked this topic as a question on
H Hg L 0 marked this topic as a question on
-
 H Hg L 0 has marked this topic as solved on
H Hg L 0 has marked this topic as solved on